자동제어의 기본개념 - 상태공간에서 제어 시스템해석
자동제어의 기본개념 - 상태공간에서 제어 시스템해석
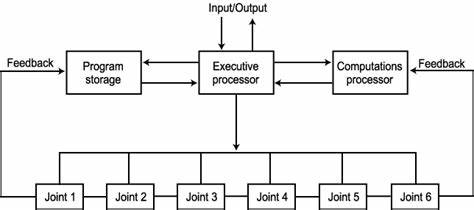
1. 상태공간에서 제어 시스템해석
1) 상태공간 표현법의 장점
① 방정식이 시간영역에서 표현된다.
② MIMO, 시변, 비선형 시스템의 해석이 가능.
2) Realization( 상태 공간 표현 ): proper 일 때만 가능

위 식을 정리하면

* 미분방정식을 상태공간으로 표현했을 때 state-space form은 유일하지 않다. 즉, 유사변화 에 의해서 원소의 배열과 행렬이 바뀔 수 있다.
* 시스템 행렬 A의 대각원소는 T(S)의 극(pole)이 된다. A의 극(pole) 즉, 고유값들을 “modes" 라하고 대각화된 행렬을 "modal form=diagonal form" 이라 한다.
* modal matrix: 고유벡터들로 이루어진 행렬
* minimal realization= 어떤 시스템이 Pole-Zero cancellations된 시스템을 realization하는 것을 말한다.
* 상태 공간 행렬들이 다음과 같을 때
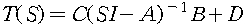
우리는 전달함수 T(S)를 packed matrix notation으로 표현할 수 있고 아래와 같다.

* 시스템의 과도 응답은 주로 극점 배치에 의해서 결정된다.
3) 가제어성과 가관측성
controllability와 observability는 고전제어와 현대제어의 기본적인 차이이다. controllability와 observability는 optimal control problem 해의 존재여부를 결정한다. 즉, 고전제어에서는 주어진 제어 사양을 제어기로 만족시킬 수 있는지 알 수 없이 trial-and-error method를 이용해서 제어사양을 만족시키도록 제어기를 설계한다. 그러나 optimal control에서는 제어사양을 만족시킬 수 있는지 여부를 controllability 와 observability로 알 수 있다. 구속조건이 없는 제어벡터에 의해, 임의의 초기상태 X(t0)에서 다른 임의의 상태로 유한 시간 내에 상태를 변화시킬 수 있다면, 시스템은 시간 t0에서 가제어(상태가제어)라고 한다. 이것은 출력 가제어와 다른개념이고 일반적으로 가제어라고 하면 상태가제어를 말한다. 초기상태가 X(t0)인 시스템에 대해 유한시간 동안 출력을 관측함으로써 이 초기 상태를 결정할 수 있으면, 이 시스템은 시간 t0에서 가관측이라고 한다. 가제어성 및 가관측성의 개념은 Kalman이 도입하였다. 이 개념은 상태공간에서의 제어 시스템의 설계에 중요한 역할을 한다. 대부분의 물리적 시스템은 가제어이고, 가관측이지만, 그에 해당하는 수학적 모델은 가제어성과 가관측성을 갖지 않을 수 있다.
① 가제어성(controllability)
입력으로 유한시간 내에서 시스템의 모든 상태변수X(t0)를 임의의 상태로 제어할 수 있을 때 controllable하다고 한다. 수학적으로 가제어성을 판단하기 위한 행렬을 controllability matrix라고 하고 아래와 같이 정의된다.
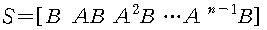
위의 S가 full rank일 때 controllable 하다고 한다.
② 가관측성(observability)
시스템의 모든 상태변수가 출력에 영향을 미칠 때 그 시스템은 observable하다고 한다. observability matrix는 아래와 같이 정의되고
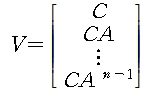
위 행렬의 rank가 full rank이면 observable하다고 한다.
가제어, 가관측성을 controllability matrix나 observability matrix를 사용하지 않고 판단하 는 방법은 시스템 행렬을 modal form 으로 해서 즉, 각각의 상태를 decouple 해서 쉽게 판단할 수 있다.
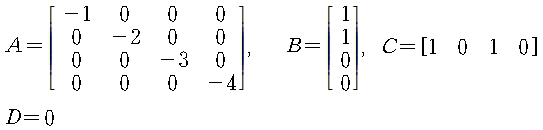
행렬 A가 대각행렬이기 때문에 Xi(i=1,2,3,4)의 controllability와 observability는 쉽게 결정된다.
X1: controllable and observable
X2: controllable but unobservable
X3: uncontrollable but observable
X4: uncontrollable and unobservable
controllable : 입력을 넣어서 우리가 원하는 출력을 얻을 수 있을 때, 입력이 각 상태에 영향을 미칠 수 있다.
observable : 출력을 가지고 상태를 알아낼 수 있는지의 여부조사, 상태 영향이 출력에 모두 영향을 미쳐야 출력을 가지고 상태를 알아낼 수 있다.
detectable : unobservable 한 모드가 stable하다.
stabilizable : uncontrollable한 모드가 stable 하다.
irreducible(coprime) : controllable하고 observable하면 irreducible하다.
시스템이 상태가제어이고 가관측일 필요충분조건은 전달함수에서 소거가 일어나지 않는 것 이다. 만약 소거가 일어나면 그 시스템은 소거된 모드 방향으로는 제어될 수 없다.
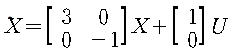
위의 방정식은 uncontrollable하다.
χ1은 controllable하고, χ2는 입력의 영향을 받지 않으므로 uncontrollable하다. 그러나 위의 시스템은 stabilize 하다. 그 이유는 uncontrollable한 모드가 stabilize하기 때문이다.
* 그러면 왜 우리는 상태공간 표현에서 가관측성과 가제어성을 중요시 여기는가?
- 가제어성 : 상태 피드백으로 시스템을 안정화시킬 수 있다.
- 가관측성 : 상태 피드백이 가지고있는 문제점은 그것이 “실용적이 아니다”라는 것이다.
즉, 모든 상태를 피드백 할 수 없는 경우( 측정이 불가능)도 있고, 상태를 피드 백 하기 위한 bandwidth의 제한이 없는 ideal sensor도 없다. 또한 많은 sensor를 사용하면 “cost"도 문제가 된다.
실제적으로는 input과 output feedback을 이용하여 상태를 예측한다.
state estimator=observer
* 가제어성과 가관측성이 모두 만족될 때 우리는 시스템을 안정화시킬 수 있다.
* 실제로 가제어성보다 약한 조건을 사용하여도 대부분의 목적에 충분하다.
* 어떤 실제적인 보상기는 보상을 위해서 측정된 시스템의 출력과 입력에 전적으로 의존하 여야 한다.
4) 현대제어 시스템의 분류
제어시스템은 두 개의 넓은 범주로 구분할 수 있다.
① regulation
외란 플랜트 매개변수의 변화 등에도 불구하고 일정한 시스템출력을 유지하 려고 한다. regulation 시스템에서는 입력을 “0”으로 한다.
② tracking
출력이 시변 입력으로 표현되는 정해진 경로를 최소 오차로 추적해야한다.
5) pole placement(state feedback)
state feedback을 이용해서 전달함수의 극(pole)을 임의의 원하는 위치로 이동시키는 것
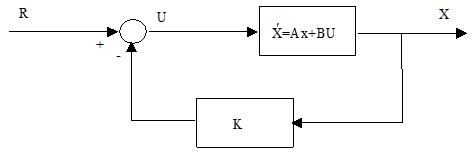
< Fig01. Control system with state feedback >
위 그림의 dynamic은 아래와 같이 표현된다.
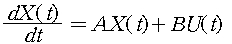
feedback gain matrix K을 통해 상태변수를 feedback 시키면 입력은

이 된다. 따라서 폐루프 시스템은 아래와 같이 표현된다.
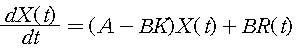
state feedback만을 가지는 시스템에서의 상태 방정식 K값을 변화시킴으로써 폐루프 시스템의 pole을 변화시킬 수 있다.
* feedback gain matrix K를 제외하고 controllability를 조사해서 “ok"이면 "K" 로 (A - BK)의 고유값을 변화시킬 수 있다.
5) observer design
5-1) estimator의 미분방정식

우리는 오차 미분방정식의 근이 빠르게 “영”으로 수렴할 수 있게 gain L을 선택하여 estimator를 설계하면 실제 시스템의 상태와 추정된 상태 사이의 오차를 “ 영”으로 줄일 수 있다.
2. estimator와 Feedback gain을 이용한 제어기설계
앞에서 언급한 feedback과 estimator를 이용해서 시스템에 적용할 수 있는 경우는 아래 와 같이 세가지 경우로 나눌 수 있다.
첫번째--- feedback만을 이용.
두번째--- estimator만을 이용.
세번째--- estimator와 feedback을 동시에 이용.
1) feedback system : feedback gain이나 estimator가 첨가되지 않은 일반적인 dynamical equation은 아래와 같다.
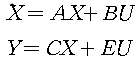
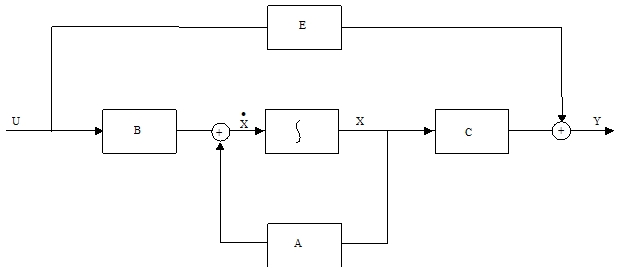
< Fig02. General dynamic system >
일반적인 시스템에 feedback gain을 첨가시키기 위해서 Plant입력을 U=R - KX이라 두면 state feedback system의 dynamical equation은 아래와 같다.
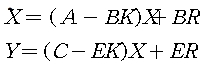
위 식을 그림으로 나타내면 다음과 같다.
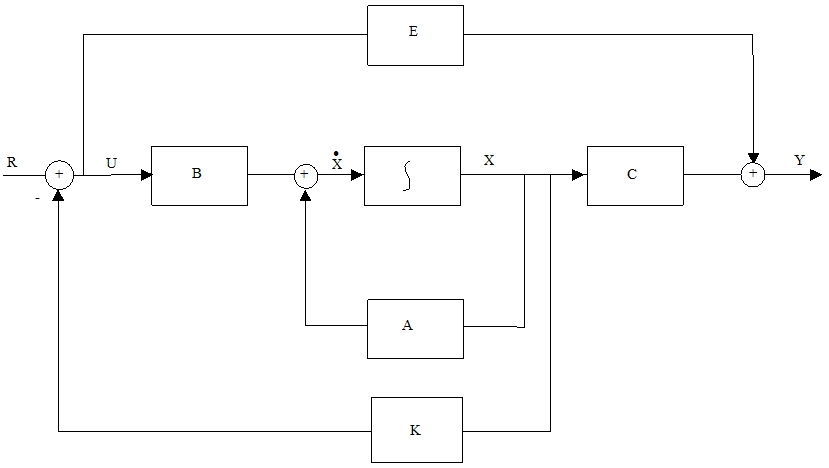
< Fig03. State feedback system >
* 입력과 출력이 각각 하나일지라도 상태는 여러 개 일 수 있다.
2) State Estimator
estimator에는 open loop estimator와 closed loop estimator로 나눌 수 있다.
① open loop state estimator
상태 출력에 의해서 공급되는 정보를 사용하지 않는다.
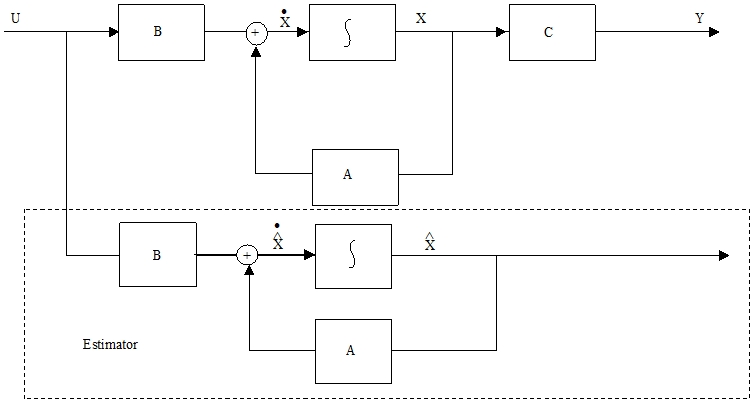
< Fig04 .Control system with open loop estimator >
* open loop estimator의 상태 방정식은
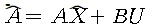
가 된다.
* 우리는 시스템의 초기조건을 알지 못한다. 만약 초기조건을 안다면 시스템 방정식의 해를 구하여 매 시간에 대한 상태들을 계산할 수 있다
* A 행렬의 고유값이 우반부에 있다면 X(t)와 X'(t)는 임의의 “t"에서 작은 오차를 가진다. 그 이유는 disturbance와 초기상태에서 잘못된 estimate 때문이다.
* open-loop estimator는 만족스럽지 못하다.
② closed loop state estimator

< Fig05. closed loop state estimator >
시스템의 출력을 관측기의 출력과 비교하여 수정 과정으로 사용한다면 오차를 안정화 시킬 수 있다. 즉, 피드백으로 안정하게 할 수 있다.
그러므로 폐루프 관측기를 이용한다.
closed loop estimator는 다음과 같다.
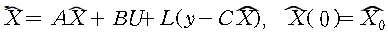
이것은 다시
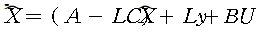
이 되고 오차 시스템에 대한 상태 방정식은 다음과 같이된다.
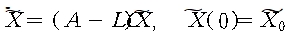
(A-LC)의 고유값이 복소 평면에 임의로 위치할 수 있도록 L을 선택한다면 오차에 대 한 문제를 해결할 수 있다. 즉, 관측기 오차가 어떤 초기조건에 대해서도 “0”으로 수렴 하도록 할 수 있다.
3) compensator with feedback and estimator
실제의 경우 위에서 언급한 것처럼 feedback gain과 estimator를 따로 사용하지 않고 같이 사용한다. 그 그림은 아래와 같다.
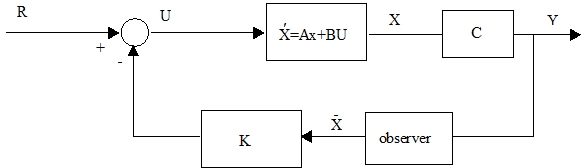
< Fig06. Control system with observer and state feedback >
설계 절차는 아래와 같다.
① feedback system에서 K를 결정한다. 이때 estimator는 무시한다.
② estimator에서 L을 선택한다. 이때 feedback system은 무시한다.
③ 추정된 상태를 feedback gain의 입력으로 한다.
④ 제어기 극점의 선택과 마찬가지로 관측기 극점은 추정공정의 빠른 수렴성을 확보하 기 위해서 제어기 극점보다 몇 배 빨라야한다.
3-1) 분리 특성( Separation property )
제어 문제와 관측기 문제의 분리 : 즉, 상태들이 이용 가능하다고 가정하고 제어기 이득을 찾은 다음 이 상태들을 추정하기 위해서 관측기를 설계하고 상태들 대신에 추정값을 사용할 수 있다. 시스템의 폐루프 극점은 제어기 극점과 관측기 극점의 합집합이다.
예측된 상태를 feedback 시키면 입력은
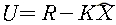
이 된다. 시스템의 상태방정식에 예측된 상태를 가지는 plant입력 U를 대입하면

위의 식은 다음과 같이 된다.

In other words, the set of poles of combined system consists of the union of the control poles and the estimator poles. This means that the designs of the control law and the estimator can be carried out independently.
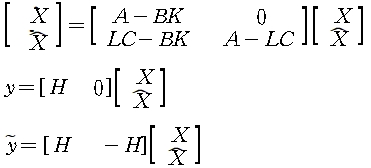
3-2) K, L을 구하는 법
특성방정식의 근이 2차인 경우 쉽게 구할 수 있으나 그 이상의 차수에서는 구하기가 어렵다.
※ 2차인 경우
- feedback system
feedback system의 상태공간 표현은
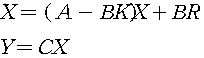
이므로 Det(A - BK) = 0 근의 위치를 정한다(pole placement).


SISO인 경우에 matlab에서 acker을 사용하고 MIMO인 경우에는
place명령을 사용한다.
https://electriceng.tistory.com/1170
자동제어의 기본개념 - 블럭 다이어그램
자동제어의 기본개념 - 블럭 다이어그램 1. 제어시스템1) 분류고전제어 이론이 단지 선형 시불변(LTI) 일입력 일출력(SISO) 시스템에만 적용될 수 있는 반면에, 현대 제어이론은 선형, 비선형,
electriceng.tistory.com
https://electriceng.tistory.com/1171
자동제어의 기본개념 - 주파수 응답해석
자동제어의 기본개념 - 주파수 응답해석 1. 주파수 응답해석 2차 시스템의 시간응답은 폐루프 주파수 응답의 Mr과 ωr을 구함으로써 정확하게 예측할 수 있다. 고차 시스템에서는 이들의 상
electriceng.tistory.com
https://electriceng.tistory.com/1172
자동제어의 기본개념 - 보상기
자동제어의 기본개념 - 보상기 1. 보상기1) S-평면의 좌반부에 있는 pole-zero는 cancel 해도 되지만 우반부의 있는 pole-zero는 cancel 하지 말아야한다. 그 이유 중 하나는 우반부의 pole-zero는 실제시스템
electriceng.tistory.com
https://electriceng.tistory.com/1174
자동제어의 기본개념 - Lyapunov 안정도 해석
자동제어의 기본개념 - Lyapunov 안정도 해석 1. Comments regarding state space design개루프의 pole, zero가 어디에 위치하든지 폐루프의 pole을 임의의 위치로 이동시킬 수 있다. 제어설계의 관점에서 obs
electriceng.tistory.com
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 변압기 보호계전방식의 종류 (0) | 2024.05.21 |
|---|---|
| 자동제어의 기본개념 - Lyapunov 안정도 해석 (0) | 2024.05.20 |
| 자동제어의 기본개념 - 보상기 (0) | 2024.05.16 |
| 자동제어의 기본개념 - 주파수 응답해석 (1) | 2024.05.14 |
| 자동제어의 기본개념 - 블럭 다이어그램 (0) | 2024.05.13 |






