자동제어의 기본개념 - Lyapunov 안정도 해석
자동제어의 기본개념 - Lyapunov 안정도 해석

1. Comments regarding state space design
개루프의 pole, zero가 어디에 위치하든지 폐루프의 pole을 임의의 위치로 이동시킬 수 있다. 제어설계의 관점에서 observers는 stability margin을 줄인다. reduced order observer는 bandwidth를 증가시킴으로 인해서 시스템을 high-frequency noise에 민감하게 한다. 이런 문제에 대한 해결책으로 robust control을 사용한다. 처음에는 고전적인 방법으로 제어시스템을 설계한 후 결과가 만족스럽지 않으면 그후 상태공간 방법으로 제어 시스템을 설계해야한다.
1) proper , improper

① finite constant => proper
② zero => strictly proper
③ ∞ => improper
* 대부분의 실제 시스템은 strictly proper 하다.

2)well-posedness
G1(S) ,G2(S)가 proper이고, 어떤 두점 사이의 전달함수도 proper 이어야한다.
2. Lyapunov 안정도 해석
제어 시스템에서 안정도는 가장 중요하다. 시스템이 선형이고 시불변이면 많은 안전도 판별법의 적용이 가능하다. 그 중에는 Nyquist 안정도 판별법과 Routh 안정도 판별법이 있다.
그러나 시스템이 비선형이거나 또는 선형이더라도 시변이면 앞의 판별법의 적용이 불가능하다.

위 식의 Lyapunov function을 정의하면

이 된다. 여기서 M은 positive definite matrix

< Fig01. A Lyapunov function V(X) >

위의 식을 Lyapunov equation이라 하고, 위 식을 만족하는 M이 존재할 때 안정하다고 할 수 있다.
* Lyapunov equation을 어떠한 방법으로 푸는가에 대한 논문도 많다.
3. Digital Control

< Fig02. Digital control system >

< Fig03. Digital control system >
1) 차분 방정식
continuous system에서는 Dynamic equation이 미분 방정식에 의해서 표현되고 digital system에서는 차분 방정식에 의해서 표현된다.
linear nth-order difference equation

state equation
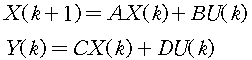
2) Z-Transform

T=sampling time
3) Solution of Difference Equation
① sequential procedure
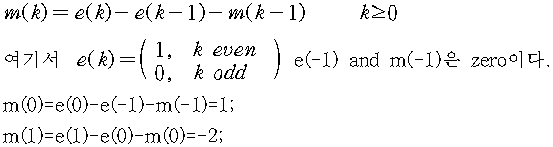
② Z-Transform
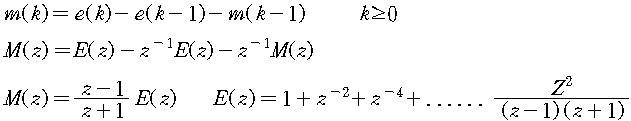
3) State Variable
아래와 같은 차분방정식이 주어질 때

4. Sampling and Reconstruction
1) Sampling theorem

여기서 ωo는 원래 신호의 highest frequency,
@ Zero-order-hold의 전달함수

< Fig04. 임펄스 입력에 의한 Zohdml 응답 >
※ Zohdml 응답

S-Plane의 좌반부에 있는 점들은 모두 Z-Plane의 크기가 “1”인 원 내부로 모두 매핑 된다.
5. Numerical Integration Methods
analog filters를 등가인 digital filters로 변환할 때 가장 중요한 것은 주파수응답을 최대한 일치시키도록 해야한다. forward Euler, backward Euler, trapezoidal 등의 방법이 있다.
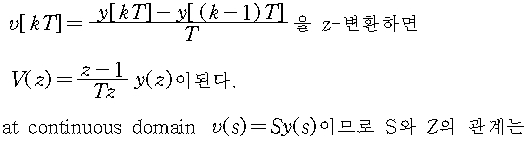

Trapezoidal transformation은 “ bilinear or Tustin's " transformation이라 알려져 있다.
Tustin's transformation은 아날로그 필터를 디지털 필터로 전환하는 가장 일반적인 방법이다.
forward Euler technique does not always preserve stability
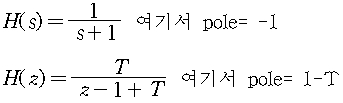
만일 T가 2보다 크면 pole은 단위원 바깥에 존재하여 unstable 하다.
Tustin은 warping의 문제를 가지고 있다.
frequency scale is distorted(warping)
6. Digital Control Design
1-1) Design Continuous compensation
1-2) Digitization continuous compensation
2) Direct Design digital compensator using frequency transform
3) Direct Design digital compensator using state space
7. PID
1) analog
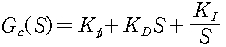
2) discrete
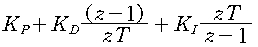
예)
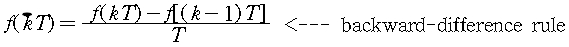
위의 식을 Z-변환하면

8. w-transform
앞에서 언급한 것처럼 digital 보상기를 설계하는데는 continuous 설계방법과 직접적으로 Z-domain에서 설계하는 방법이 있다. Z-domain에서 설계는 단위원안에서 행해지므로 어려움이 있고, 특히 bode 선도기법은 사용할 수 없다. 그래서 S-domain 설계방법을 digital system에서 바로 적용시키기 위해 w-transform을 사용한다. 그 방법은 G(S)--> G(Z)-->G(W)로 변환해서 우리가 알고있는 설계기법을 이용한다.
9. SISO의 digital 제어 예제
22-1) 디지털제어의 구현 : 실제 구현을 할 경우 보상기는 컴퓨터에 차분방정식의 형태로 프로그래밍 된 것에 해 당하고, plant는 hardware로 구성된다. 그러나 이와 같이 차분방정식으로 보상기가 프로그래밍 된 경우 시스템의 안정도를 알 수 가 없다. 그래서 Z-변환을 해서 안정도를 확인하여야 한다.
22-2) simulation : digital system의 simulation은 안정도와 동작상태를 알고자하는 것이 목적이다.
① step response
siso시스템(ex1)의 plant 전달함수
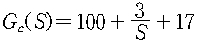
step response를 알기 위해서 가장먼저 S-domain에서 Z-domain으로 각각의 전달함수 를 변환시켜야한다. 제어기의 전달함수는 주파수특성이 중요하므로 “tustin"방법으로 Z-domain으로 변환시키고, plant는 step response의 특성이 중요하므로 ”zero-order-equivalence"방법으로 변환시킨다.
G(Z) = Gc(Z)Gp(Z)라 할 때 step response를 보기 위한 simulation은 아래 그림과 같다.

< Fig05. ex3-1 Step respose block >
- sampling time을 각각 0.01초로 했을 때의 0.1초로 했을 때의 출력은 다음과 같다.

< Fig06. ex3-2, step response with sampling time at 0.01sec and 0.1 sec >
② bode 선도
Z-domain에서는 bode선도를 이용하지 못하므로 W-transform을 하여 bode 선도를 그린다. sampling time=0.01초 일 때의 bode 선도는 다음과 같다.

< Fig07. ex3-3. bode 선도 sampling time =0.01sec
③ sine response
- sampling time을 각각 0.01초로 했을 때와 0.1초로 했을 때의 출력은 다음과 같다.

< Fig08. ex3-3. sine response with sampling time at 0.01sec and 0.1sec >
https://electriceng.tistory.com/1170
자동제어의 기본개념 - 블럭 다이어그램
자동제어의 기본개념 - 블럭 다이어그램 1. 제어시스템1) 분류고전제어 이론이 단지 선형 시불변(LTI) 일입력 일출력(SISO) 시스템에만 적용될 수 있는 반면에, 현대 제어이론은 선형, 비선형,
electriceng.tistory.com
https://electriceng.tistory.com/1171
자동제어의 기본개념 - 주파수 응답해석
자동제어의 기본개념 - 주파수 응답해석 1. 주파수 응답해석 2차 시스템의 시간응답은 폐루프 주파수 응답의 Mr과 ωr을 구함으로써 정확하게 예측할 수 있다. 고차 시스템에서는 이들의 상
electriceng.tistory.com
https://electriceng.tistory.com/1172
자동제어의 기본개념 - 보상기
자동제어의 기본개념 - 보상기 1. 보상기1) S-평면의 좌반부에 있는 pole-zero는 cancel 해도 되지만 우반부의 있는 pole-zero는 cancel 하지 말아야한다. 그 이유 중 하나는 우반부의 pole-zero는 실제시스템
electriceng.tistory.com
https://electriceng.tistory.com/1173
자동제어의 기본개념 - 상태공간에서 제어 시스템해석
자동제어의 기본개념 - 상태공간에서 제어 시스템해석 1. 상태공간에서 제어 시스템해석1) 상태공간 표현법의 장점① 방정식이 시간영역에서 표현된다.② MIMO, 시변, 비선형 시스템의 해석이
electriceng.tistory.com
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 변압기(단상)의 병렬운전 구비조건 (0) | 2024.05.22 |
|---|---|
| 변압기 보호계전방식의 종류 (0) | 2024.05.21 |
| 자동제어의 기본개념 - 상태공간에서 제어 시스템해석 (0) | 2024.05.17 |
| 자동제어의 기본개념 - 보상기 (0) | 2024.05.16 |
| 자동제어의 기본개념 - 주파수 응답해석 (1) | 2024.05.14 |






