자동제어의 기본개념 - 블럭 다이어그램
자동제어의 기본개념 - 블럭 다이어그램

1. 제어시스템
1) 분류
고전제어 이론이 단지 선형 시불변(LTI) 일입력 일출력(SISO) 시스템에만 적용될 수 있는 반면에, 현대 제어이론은 선형, 비선형, 시불변, 시변인 다입력 다출력(MIMO) 시스템에 적용될 수 있다.
① 고전제어: Laplace Transform, 전달함수, 주파수 해석을 통한 제어
② 현대제어: 실시간 제어, 상태방정식, 시간 해석을 통한 제어
2) 상태
상태(state)는 t=t0에서 변수를 알고, t≥t0에서 입력을 알면 t≥t0에서 시스템의 거동을 완전히 결정할 수 있을 때, 이러한 변수(상태변수)들의 최소 집합이다. 따라서, 시간 t에서 동적 시스템의 상태는 시간 t0에서의 상태와 t≥t0에서의 입력으로부터 유일하게 결정될 수 있다.
3) 상태변수
상태변수는 물리적으로 측정될 수 있거나 관측될 수 있는 양일 필요는 없다. 그러나 가능하다면 쉽게 측정할 수 있는 양을 상태변수로 선택하는 것이 편리하다.
4) 전달함수
선형 시불변 시스템의 전달함수는 모든 초기 조건들이 “영”이라는 가정하에서 출력의 Laplace 변환식과 입력의 Laplace 변환식의 비

여기서 R(S)는 입력의 Laplace Transform , Y(S)는 출력의 Laplace Transform 이다.
2. 블럭 다이어그램(Block diagram)
제어계의 구성이나 상호연결관계를 블럭으로 나타낸 그림
1) open loop

< Fig01. 1 open loop >
X3(S) = G2(S)G1(S)X1(S)
2) closed loop

< Fig02. closed loop >
① 개루프 전달함수(open-loop)
되먹임 신호B(S)와 작동오차 신호 E(S)의 비를 개루프 전달함수라고 한다.

② 폐루프 전달함수 (closed-loop)
E(S)=R(S)-H(S)Y(S)
Y(S)=G(S)E(S)
=G(S)[ R(S)-H(S)Y(S) ]
Y(S)[ 1+G(S)H(S) ]=G(S)R(S)
위 식을 전달함수로 나타내면

가된다.
3) 외란을 받고 있는 폐루프 시스템
두 개의 입력(기준입력과 외란)이 선형시스템에 작용할 때 각각의 입력을 독립적으로 취급할 수 있다. 즉, 각각의 입력에 대한 출력을 따로 계산하여 더해주면 전체의 출력이 된다.

< Fig03. 외란을 받고 있는 폐루프 시스템 >
외란 N(S)의 영향을 검토하기 위해서는 시스템의 오차가 “0”으로 정지해있고 단지 외란 만이 작용한다고 가정하여 응답을 계산하면 되고 아래와 같다.
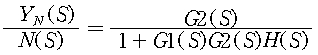
반면에 기준입력 R(S)에 대한 응답을 고려하기 위해서는 외란을 “0”으로 가정하고 응답을 구하면 된다.
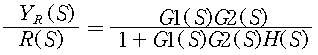
기준입력과 외란이 동시에 작용할 때 응답은 위의 두 응답을 합치면 된다.
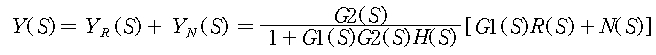
3. 신호 흐름선도(signal-flow-graphs)
시스템의 블럭선도가 복잡해짐으로써 전달함수를 구하는 것이 어려워진다. 그래서 mason의 공식을 이용하여 복잡한 블록선도를 가지는 시스템의 전달함수를 간단히 구할 수 있다.

< Fig04. Signal Flow Graph >
Masion 정리: 신호 흐름선도의 전체 전달함수
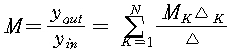
N=Total number of forward paths between yin and yout

4. 물리계의 수학적 모델
1) 제어계통의 모델화
① 전달함수: 선형 시불변계 (LTI: Linear Time Invariant)
② 상태방정식: 시변, 시불변, 비선형
2) Dynamic equation
① 상태방정식
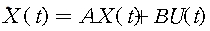
② 출력방정식
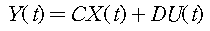
3) Dynamic equation -> 전달함수
Laplace Transform을 시변 시스템에서는 적용이 불가능하다. 상태방정식을 Laplace Transform하면

이다. 위 식을 정리하여 전달함수를 구하면 아래와 같다.

4) 비선형 수학적 모델의 선형화
선형화 절차는 비선형 함수를 작동점 부근에서 Taylor급수로 전개한 후 선형항만을 취하는 것이다. Taylor급수전개에서 고차항들은 무시하기 때문에 이 무시된 항들은 충분히 작아야한다. 즉, 변수들은 작동점으로부터 크게 벗어나지 않아야 한다.
5. 제어 계통의 시간영역 해석
제어 시스템을 해석하고 설계하는 데 있어서 여러 가지 제어시스템의 성능을 비교하는 기준이 있어야한다. 이러한 기준으로서 특별한 시험입력신호를 정하고 그 입력신호에 대해서 여러 시스템의 응답을 비교하곤 한다. 시험입력신호로 보통 사용되는 것은 계단(step)함수, 램프(ramp)함수, 포물선(parabolic)함수, 임펄스(impulse)함수, 사인파(sinusoidal)함수가 있다. 이러한 시험신호들은 시간에 대해 매우 단순한 형태의 함수이므로, 이 시험신호들을 이용하면 제어시스템을 수학적으로나실험적으로 쉽게 해석할 수 있다. 시스템 특성을 해석하는데 어느 신호를 선택할 것인가는 그 시스템의 입력이 정상 동작 하에서 주로 어떤 형태인가에 달려있다.
· 과도 응답 : 응답시 시간이 지남에 따라 사라지는 성분 -> 안정도가 중요
· 정상 응답 : 과도기간이 지난후에 남아있는 성분 -> 정상상태 편차가 중요
1) 정상상태 편차(ESS)
그림(Fig02)에서 오차신호 E(S)를 구하면 아래와 같다.

2) 민감도(Sensitivity)
공정 전달 함수의 백분율 변화에 대한 시스템 전달함수의 백분율 변화의 비
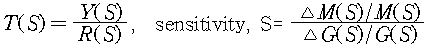
3) DC gain
주파수영역에서는 주파수가 “0” 일 때의 이득이고 시간영역에서는 정상 상태에서 입력과 출력과의 비
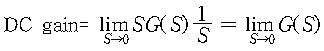
4) 단위 계단 응답과 시간영역성능
과도 응답
① 1차 시스템(First order system)
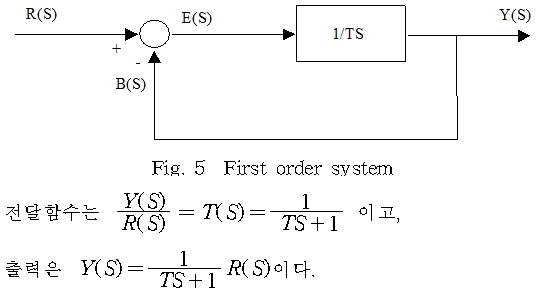

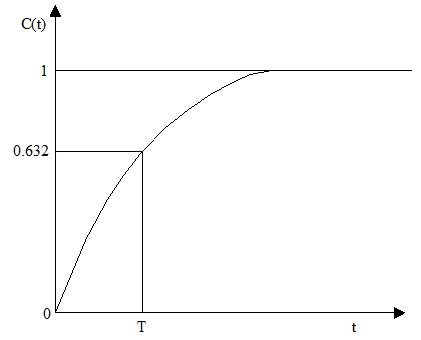
< Fig06. Step response of first order system >
1차계의 전달함수에서
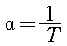
라 하면 아래와 같이 변환된다.
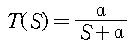


< Fig07. Frequency Response of first order system >
② Unit-Step Response and Time-Domain specification

< Fig08. Step response >
· 최대 오버슈트(maximum overshoot)
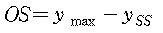
· 퍼센트 오버슈트
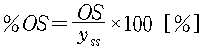
· 지연시간ta(Delay time): 최종치의 50%에 도달하는 시간
· 상승시간tr(rising time): 최종치의 10%- 90%까지 도달하는시간
· 정정시간ts(settling time): 최종치의 특정백분율(대개 5%)에 도달하는 시간
5) 원형 2차 계통 (Prototype Second-order system)
실제 2차 시스템은 흔치않다. 그러나 2차 시스템을 이해함으로써 다른 고차의 시스템을 이해할 수 있다. 고차 시스템도 2차로 근사화해서 설계할 수 있다.
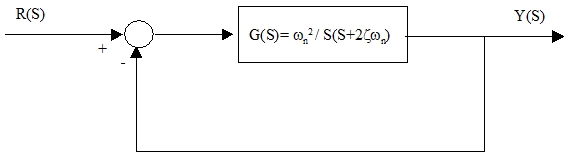
< Fig09. Second-order System >
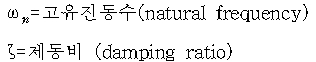


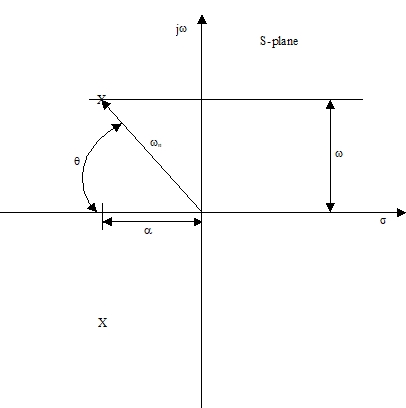
< Fig10. Relationship between the characteristic-equation roots and a,wn, w >
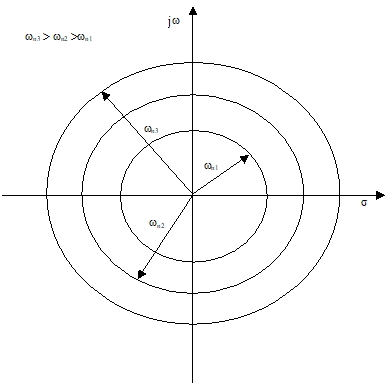
< Fig11. Constant-natural-undamped-frequency loci >

< Fig12. Constant-damping-ratio loci >
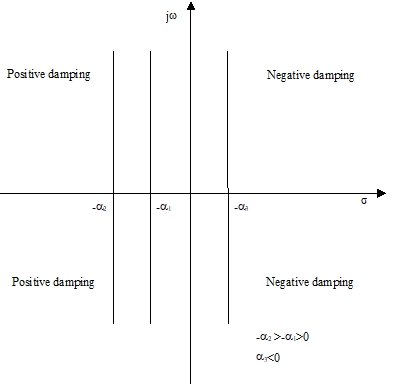
< Fig13. Constant-damping-ratio loci >
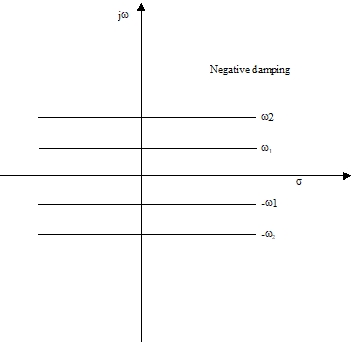
< Fig14. Constant-conditional-frequency loci >
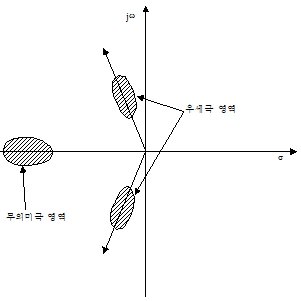
< Fig15. Effect on poisition of pole >
6) 전달함수에서의 우세극
① 무의미극
실수부의 크기가 우세부 실수부의 5-10배 되어 과도기 상태에서 빠른 감쇠를 보인다. 허수축에서 너무 멀리 떨어져있으면 실제적으로 하드웨어 제작이 불 가능한 경우도 있다.
② 우세극
계통의 동적 특성을 제어하기 위한 영향력 있는 pole 즉, dominant pole
* 무의미극 즉, 허수축에서 멀리 떨어질수록 많은 에너지가 필요로 한다.
* 전달함수의 zero가 허수축에 가까울수록 overshoot가 커진다.
자동제어의 기본개념 - 주파수 응답해석
자동제어의 기본개념 - 주파수 응답해석 1. 주파수 응답해석 2차 시스템의 시간응답은 폐루프 주파수 응답의 Mr과 ωr을 구함으로써 정확하게 예측할 수 있다. 고차 시스템에서는 이들의 상
electriceng.tistory.com
https://electriceng.tistory.com/1172
자동제어의 기본개념 - 보상기
자동제어의 기본개념 - 보상기 1. 보상기1) S-평면의 좌반부에 있는 pole-zero는 cancel 해도 되지만 우반부의 있는 pole-zero는 cancel 하지 말아야한다. 그 이유 중 하나는 우반부의 pole-zero는 실제시스템
electriceng.tistory.com
https://electriceng.tistory.com/1173
자동제어의 기본개념 - 상태공간에서 제어 시스템해석
자동제어의 기본개념 - 상태공간에서 제어 시스템해석 1. 상태공간에서 제어 시스템해석1) 상태공간 표현법의 장점① 방정식이 시간영역에서 표현된다.② MIMO, 시변, 비선형 시스템의 해석이
electriceng.tistory.com
https://electriceng.tistory.com/1174
자동제어의 기본개념 - Lyapunov 안정도 해석
자동제어의 기본개념 - Lyapunov 안정도 해석 1. Comments regarding state space design개루프의 pole, zero가 어디에 위치하든지 폐루프의 pole을 임의의 위치로 이동시킬 수 있다. 제어설계의 관점에서 obs
electriceng.tistory.com
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 자동제어의 기본개념 - 보상기 (0) | 2024.05.16 |
|---|---|
| 자동제어의 기본개념 - 주파수 응답해석 (1) | 2024.05.14 |
| 한전 관로공사 설계기준 (DS-5200) - 관로 도통시험 등 (0) | 2024.05.10 |
| 한전 관로공사 설계기준 (DS-5200) - 관로설치 (0) | 2024.05.09 |
| 전기설비 보호계전 시스템 Chapter.04 - 고조파 억제회로부 비율차동 계전기 (0) | 2024.05.08 |






