회로이론 - 대칭좌표법
회로이론 - 대칭좌표법

1. 개요
3상 단락고장처럼 각 상이 평형된 고장에서는 고장점을 중심으로 여기에 인가된 전압과 임피던스를 구해서 쉽게 해석할 수 있다. 그러나 각 상이 불평형이 되는 1선지락과 탕은 불평형 고장에서는 각 상에 걸리는 전압을 따로따로 구해야 하는데 실제적으로는 이것이 그 해를 구하기가 어렵워진다. 따라서 대칭좌표법(불평형 3상전류의 각 상을 영상전류, 정상전류, 역상전류 등 새로운 Vector로 치환, 이를 이용하여 고장전류를 구하는 방법)을 이용하지 않고서는 불평형문제를 다룰 수 없다.
대칭좌표법은 불평형의 전류나 전압을 그대로 취급하지 않고 일단 그것을 대칭적인 3개의 성분으로 나누어서 각각의 대칭분이 단독으로 존재하는 경우의 계산을 실시한 다음 마지막으로 그들 각 성분의 계산결과를 중첩시켜서 실제의 불평형인 값을 알고자 하는 방법이다.
그러므로 계산도중에는 언제나 평형회로의 계산만 하게 되고 각 성분의 계산이 끝난 다음 이들을 중첩함으로써 불평형 문제의 해가 얻어지는 것이다.
2. 정의
아래의 식에서(각 전압과 전류의 성분은 벡터임)
1) 고장시의 전류

2) 영상전압, 영상전류

동일한 크기와 위상각을 가진 평형단상전류로서 영상전류(전압)라고 부른다. 이 영상전류는 지락고장시 접지계전기를 동작시키는 전류이지만, 통신선에 유도장해를 일으키는 전류이기도 하다.
3) 정상전압, 정상전류
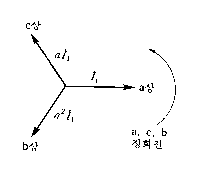
평형 3상 교류로서 전원과 동일한 상회전 방향으로 포함되어 있는 전류로 이 전류가 전동기에 흐르면 전동기에 회전토크를 발생시킨다.
4) 역상전압, 역상전류

상회전이 반대인 3상 평형전류로서 이 전류가 전동기에 흐르면 제동작용을 해서 그 만큼 전동기의 출력을 감소시키게 된다.
3. 대칭분전압
1) 각상전압
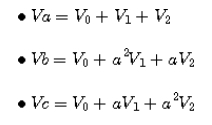
행렬식으로 표현하면

2) 대칭분 전압(Va 기준)
a 상을 기준으로 전압 Va, Vb, Vc라고 하면, a 상을 기준으로 한 대칭분
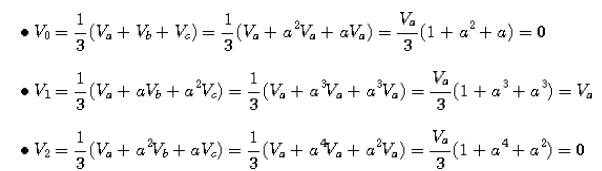
행렬식으로 표현하면
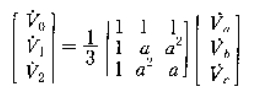
4. 대칭분전류

1) 각 상전류

2) 대칭분 전류(Ia 기준)

행렬식으로 표현하면

5. 위상차
여기서 a, a2은 각각 벡터이기 때문에 가령 Ib에 a를 곱한다는 것은 Ib라는 전류의 위상을 120도 만큼 앞서게 한다는 것이고 a2을 곱하면 그 전류를 240도 만큼 앞서게 한다는 것이다. 그러므로 Ia, Ib, Ic가 불평형전류라 하여도 이것이 주어지면 여기에 a, a2 등을 곱해서 쉽게 구할 수 있다.

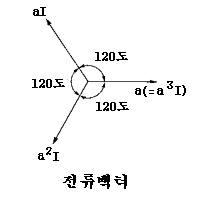
6. 발전기의 기본식

그림과 같은 3상 발전기에서 발전기가 임의의 불평형 전류를 흘리고 있을 경우 그 단자전압과 전류와의 관계를 구해 본다. 단, 발전기는 대칭이고 무부하 유도전압은 3상이 평형되고 있다.
지금 Ea, Eb, Ec를 각 강의 무부하 유도전압 va, vb, vc를 각 상의 전압강하라고 하면, a,b,c 각 상의 단자전압 Va, Vb, Vc는


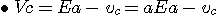
로 표현된다.
따라서 이들 대칭분은 상기의 식 및


이라는 관계를 이용하면
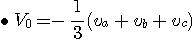

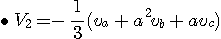
로 된다.
여기서 전기자 전압강하를 계산하기 위하여 먼전 영상전류만을 흘렸을 경우를 생각하면 각 상의 전압강하는 동일해서 Z0와 I0의 곱으로 된다. 이처럼 Z0는 발전기에 영상전류인 동상의 전류가 각 상에 흘렀을 때의 임피던스로서 이것을 발전기의 영상임피던스라고 한다. 단, 여기서 Z0 이외의 임피던스는 I0에 의해서 전압강하를 발생하지 않는 것으로 하고 있다.
다음에 각 상에 I1, a2I1, aI1인 정상의 3상 평형전류를 흘렸을 경우 전압강하는 Z1I1, a2Z1I1, aZ1I1으로 된다. 여기서 Z1은 정상의 3상 평형전류를 흘렸을 경우의 임피던스로서 이것을 발전기의 정상임피던스라고 한다. 또한, 이것은 발전기의 명판에 적혀있는 동기임피던스이다.
마지막으로 각 상에 I2, aI2, a2I2 인 역상의 3상 평형전류를 흘렸을 경우 임피던스강하는 각각 Z2I2, aZ2I2, aZ2I2 , a2Z2I2로 된다. 여기서 Z2는 역상의 3상 평형전류가 흘렀을 경우의 임피던스로서 이것을 발전기의 역상임피던스라고 한다.
실제로 전기자 전압강하는 이들의 대칭분 전류가 흘렀을 경우 각 상분의 전압강하를 중첩시켜서 구할 수 있다. 즉,



로 되고, 이것으로부터 다음의 식을 얻는다.
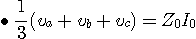
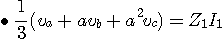

따라서 위의 두식을 대입하면
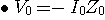


로 정리되는데 이것을 발전기의 기본식이라고 한다.
이 빌전기의 기본식을 이용함으로써 어떠한 불평형전류가 주어지더라도 쉽게 이때의 회로 계산이 가능하다. 가령 어떤 불평형전류가 주어지면 그것으로부터 I0, I1, I2의 각 대칭분을 만들 수 있으며, 이것을 발전기의 기본식에 대입함으로써 이때 발전기의 단자전압에 나타나는 전압의 대칭분 V0, V1, V2를 구할 수 있다. 이렇게 해서 대칭분 전압이 구해지면 그 뒤에는
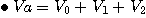


의 식을 이용해서 실제로 알고자 하는 각 단자에서의 전압 Va, Vb, Vc의 값을 알 수 있게 되는 것이다.
반대로 발전기의 단자에 불평형 전압이 주어진 경우 발전기에 어떠한 불평형전류가 흐르게 되는가 하는 것도 발전기 기본식을 이용하여 쉽게 구할 수 있다. 이처럼 대칭좌표법을 이용하면 불평형고장시의 단자전압 계산이 가능하다.
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 회로이론 - 분포정수회로 (0) | 2021.10.05 |
|---|---|
| 회로이론 - 왜형파 (0) | 2021.10.04 |
| 회로이론 - 다상교류 (0) | 2021.09.30 |
| 회로이론 - 회로망 (1) | 2021.09.29 |
| 회로이론 - 결합회로 (0) | 2021.09.28 |






