회로이론 - 회로망
회로이론 - 회로망
1. 전원
1) 전압원

실제 전압원 : 내부저항을 포함하는 전압원(전압강하가 발생한다)
이상 전압원 : 내부저항이 0인 전압원(전압강하가 발생하지 않으므로 전압은 항상 일정하다)
2) 전류원

실제 전류원 : 내부저항을 포함하는 전류원
이상 전류원 : 내부저항이 ∞ 인 전류원
3) 등가회로
그림의 전압원과 그림 전류원은 서로 등가이다.

2. 키르히호프의 법칙(Kirchhoff's law)
회로망의 전압이나 전류의 분포를 결정하는데 가장 중요한 기본적 법칙이다.
옴의 법칙에서 발전한 것으로서 전류에 관한 제1법칙과 전압강하에 대한 제2법칙이 있다.
1) 제1법칙(전류법칙 : K·I·L)
들어가는 전류와 흘러나오는 전류의 합은 0이다 이것을 식으로 표시하면
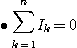
이 된다.
2) 제2법칙(전압법칙 : K·V·L)
회로망 내의 임의의 폐회로에 들어있는 저항에 생기는 전압강하의 합은 그 폐회로 속에 들어있는 기전력의 합과 같다. 이것을 식으로 표시하면

이 된다.
3. 중첩의 원리(Principle of superposition)
선형회로망 내에 다수의 기전력이 동시에 존재할 때 회로전류는 각 기전력이 각각 단독으로 그 위치에 존재할 때에 흐르는 전류의 합이다.
4. 데브난의 정리( Thevenin's Theorem)
2개의 독립된 회로망을 접속하였을 때의 전압, 전류, 임피던스의 관계를 나타내는 정리

개방끝 a,a'에 전압이 있을 때 단자 b,b'를 접속하면 a,b사이에 흐르는 전류는 다음과 같이 나타낸다

5. 노튼의 정리
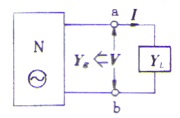
데브난의 정리를 적용하면 복잡한 실제적 문제를 해결할 때 등가회로망의 임피던스를 결정하는 것이 곤란한 경우가 있다. 이 경우 폐회로 전압(V)을 단락전류(B회로)로 나누어 임피던스를 구하는 것이 편리하다.
노튼의 정리로 부하전류를 구하면(벡터 값임)
I = V/(Za+Zb) = V/{(V/단락전류)+B회로의 임피던스)} = (Yb ·Is)/(Ya+Yb)
6. 밀만의 정리(Millnan's Theoren)
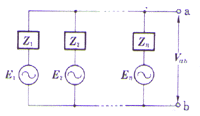
내부 임피던스를 가진 전압원이 여러 개 병렬로 되어 있을 때 합성전압은 개개의 전압원을 단락했을 때 흐르는 전류의 총합을 개개 전원의 어드미턴스의 총합으로 나눈 것과 같다.
즉, 합성전압 = 개개의 전압원을 단락시 흐르는 전류의 총합/개개 전원의 어드미턴스의 총합
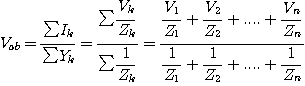
7. 상반(相反)의 정리 : Reciprocity Theorem - 가역정리

내부에 전원을 갖지 않는 임의의 회로에서 j번째의 망로(網路)에 Vj의 전압을 가했을 때 K번째의 망로에 Ik의 전류가 흐르고, 같은 회로에 있어서 K번째의 망로에 Vk의 전압을 가했을 때 j번째의 망로에 Ij의 전류가 흘렀을 경우 VjIj=VkIk가 성립한다는 정리를 말한다. 또 Vj = Vk이면 Ij = Ik가 된다.
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 회로이론 - 대칭좌표법 (0) | 2021.10.01 |
|---|---|
| 회로이론 - 다상교류 (0) | 2021.09.30 |
| 회로이론 - 결합회로 (0) | 2021.09.28 |
| 회로이론 - 교류전력 (0) | 2021.09.27 |
| 회로이론-직류회로 / 교류회로 (0) | 2021.09.20 |






