교류회로 (Alternating Current Circuit)의 해석
교류회로 (Alternating Current Circuit)의 해석

오늘은 교류회로 (Alternating Current Circuit)에 대해 포스팅하겠습니다.
전류는 크기와 방향의 변화에 따라 3가지로 나눌 수 있습니다.

이 그래프는 우리가 많이 다뤘던 직류(Direct Current)의 전류 그래프입니다.
실생활에서는 건전지, 축전지, 정류기등 저장을 할 수 있는 소자에 사용하는 일이 많습니다.
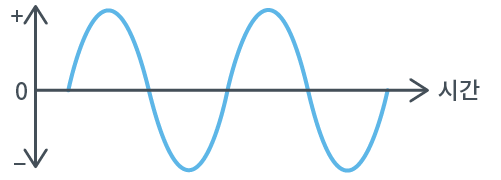
이 그래프는 교류(Alternating Current)의 전류 그래프입니다.
교류는 직류처럼 저장이 불가능하기 때문에, 생산과 동시에 소비 해야하는 특징이 있습니다.
따라서, 우리가 가정에서 교류전압을 사용할 때 전선이 꼭 있어야 합니다.
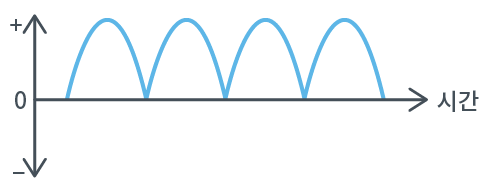
이 그래프는 처음 보실텐데, 맥류(Pulsating Direct Current)라고 합니다.
보통, 교류를 다이오드를 이용한 정류(Rectification)회로로 처리함으로 얻을 수 있습니다.
실생활에서는 전화기의 음성으로 사용하고 있습니다.
※ 에디슨과 테슬라의 전류전쟁
에디슨은 필라멘트 전구를 발명하고, 이를 상용화하며 발명가와 경영자의 일을 모두 잘하는 수완가였습니다.
이 때, 에디슨이 사용하던 방식이 직류 송전방식이었습니다.
초기의 직류전압은 기초 전압이 낮아 높은 전압을 얻기 위해 많은 개수의 전지를 직렬로 연결해야 했고, 수명이 짧다는 단점이 있었습니다.
하지만, 전기를 멀리까지 보내기 힘들어서, 5 Km 마다 송전소를 설치해야한다는 아주 큰 단점이 있었습니다.

테슬라는 에디슨이 만든 전기회사에 입사해서 교류시스템을 개발해내었으나, 에디슨의 시기와 질투로 회사를 그만두고 다른 회사에 들어가게 됩니다.
다른 회사에서 교류의 특허권을 따낸 테슬라는 에디슨과의 경쟁을 시작합니다.

하지만, 이 과정에서 에디슨은 과장해서 사람들에게 교류에 대한 전압이 높아서 위험하다는 소문을 퍼트렸으며 언론에 지나친 비난도 서슴치 않았습니다.
시간이 지난 지금, 결국 승자는 테슬라가 되었습니다.
우리가 지금 쓰고 있는 전기는 교류시스템으로 이루어져있습니다.
아까, 직류의 단점으로 꼽았던, 전기가 멀리가지 못한다는 점이 보완가능했고, 전압을 쉽게 변화시킬 수 있었습니다.
교류의 높았던 전압은 전봇대에 있는 변압기의 의해 가정용인 220V로 떨어져서 분배됩니다.
결국, 테슬라와 에디슨의 경쟁은 테슬라의 승리로 끝나게 되었지만 이 두 명의 천재의 대결로 인해 우리 인류의 삶이 조금 더 나아졌음은 변함 없는 사실입니다.
그러면 교류에 대해 공부하기 이전에, 주파수와 주기에 대한 개념부터 짚고 넘어가겠습니다.
교류의 기본파형은 Sine 함수의 그래프인데, 이런 수학적 특징은 교류회로를 이해하는데 아주 중요합니다.
Sine 함수는 생각보다 쓸모가 많은 특징이 있습니다.
우선, Sine파가 아닌 다른 주기함수들도 서로 다른 주파수를 갖는 사인파의 합으로 나타낼 수 있습니다.
또한, 같은 주파수를 갖는 서로 다른 크기의 Sine파는 같은 주파수를 갖는 하나의 Sine파로 나타낼 수 있습니다.

x,y 평면 위에 있는 점이 반지름이 A인 원 위를 움직인다고 할 때, θ의 변화에 따른 점의 y축 길이변화의 그래프입니다.
위 그림에서, 원 위의 점이 1초동안 원운동하는 횟수를 진동수 또는 주파수 f라 정의하며 주파수의 단위는 [Hz]로 나타냅니다.
일반적으로 국내 가정용 전원으로 60Hz를 사용하는데, 이는 1초에 60번 원운동한다는 의미입니다.
이 때 원운동을 한번 하는데 소요되는 시간을 주기 T라고 하는데, 주기는 주파수의 역수의 관계를 갖습니다.
따라서 60Hz 신호는 1/60[sec]의 주기를 갖습니다.
위의 그림에서, ω라는 문자가 등장하는데 각주파수 (Angular Frequency)혹은 각속도 (Angular Velocity)라 정의합니다.
각속도는 ω = 2 π f [rad⋅Hz] = 2 π / T [rad/sec] 의 단위를 갖습니다.
예를 들어, 60HZ 신호 경우 1초동안 60회의 원운동을 하므로, 움직인 거리는 2π × 60Hz 가 됩니다.
이 값이 바로 각주파수이며, 초기 각도가 θ로 존재한다면 시간 t 동안 움직인 각도 또는 호의 길이를 ωt + θ 로 나타낼 수 있겠습니다.
또한, 반지름이 A인 원위를 움직이기 때문에 θ의 변화에 따른 원 위의 점의 y축 길이 변화는 Asineθ 가 됩니다.
이 때의 A를 진폭 (Amplitude)라고 합니다.
결국, 모두 종합하면 Sine신호의 주파수 공식은 다음과 같이 나타 낼 수 있습니다.
f(t) = Asine(ωt + θ)
정현파, 즉 Sine 함수의 크기를 나타내는 방법에는 4가지가 있는데, 이는 전자공학도라면 실험을 하다보면 이 방법으로 표현할 일이 많을것입니다.
⑴ Peak to Peak 값 : Sine파의 최댓값과 최솟값 사이 값
⑵ Peak 값 : Sine파의 최댓값
⑶ Average Value : 한 주기 동안 Sine파를 적분한 면적과 동일한 직류값

⑷ Root Mean Square (RMS) : 같은 영향을 주는 직류 값을 나타내는 교류값


'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 인덕터(Inductor)의 정의 (0) | 2020.11.11 |
|---|---|
| Semiconductor(반도체)의 정의 (0) | 2020.11.10 |
| 직류회로(Direct Current)의 해석 (0) | 2020.11.06 |
| 교류전기(AC)의 순시치/실효치/평균치/최대치 (0) | 2020.11.05 |
| 전기전자 공학단위 정리 (0) | 2020.11.04 |






