교류전기(AC)의 순시치/실효치/평균치/최대치
교류전기(AC)의 순시치/실효치/평균치/최대치

순시치와 실효치는 교류전기를 다룰 때 쓰이는 용어들입니다.
직류는 시간이 경과하더라도 크기와 방향이 일정한데
아래의 그림처럼 교류는 시간의 흐름에 따라 그 크기와 방향이 주기적으로
바뀝니다.

보통은 이러한 파형을 사인파라 하는데 360도 회전시키며 그려지는
사인(sineθ)값의 그래프와 같기 때문에 그렇습니다.
이렇게 주기적으로 변하는 값을 표기하는 방법으로는 여러 가지가 있는데
이 중에서 순시치, 실효치에 대해서만 설명합니다.
순시치는 어느 한 순간에서의 크기를 나타낼 때 사용합니다.
예를 들어 1초에 10번 주기적으로 변하는 어떤 전압이 있다면
1초가 되는 순간의 전압은 0[V]가 될 것이며 매0.1초가 되는 시점 역시도
방향이 바뀌는 지점인 0[V]가 될 것입니다.
그리고 0.1초의 1/4 지점인 0.025초 지점과 3/4지점인 0.075초 지점에서는
최대값이 될 것입니다.
(위의 그림은 최대값이 100V이므로 +100[V]와 -100[V] )
이것을 식으로 표현한다면
e=Em sinθ [V]입니다. 이것이 순시치를 나타내는 공식입니다.
sinθ를 이해하시려면 교류를 발생시키는 발전기의 원리와 회전자를 삼각함수로
표현하는 방법을 알고 계셔야 합니다.
다만, 순시치는 초당 변하는 주기 즉, 주파수와도 관계가 있기 때문에
sinθ에서 θ는 시간과 주파수가 주어지면 구할 수 있습니다.
그리고 계산의 편리성을 위하여 360˚ 방위각 대신에, 각을 원 둘레의 길이,
즉 호의 길이를 이용하여 표현하는 호도법이라는 것을 주로 사용하는데
호도법으로 표시한 각의 단위는 래디안(Radian)이라고 하며 [rad]로 표시합니다.
간단한 예로 순시치 공식을 확인해 보죠.
위에서 초당 10번 즉 10Hz, 그리고 최대치는 100[V]라 했는데
그러면 0.075초일 때 순시치가 정말로 최대값 -100[V]가 나오는지 계산해 봅시다.
θ를 호도법으로 나타내면 θ=2πf t[rad]이며, 여기서 f는 주파수, t는 시간입니다.
(θ는 발전기의 회전하고 관계가 있기 때문에 발전기의 회전자가
t초간 회전했을 때의 위치를 의미합니다.)
e=100 sin (2π·10· 0.075) = 100 sin 4.71238898 = 100 * (-1) = -100[V]
으로 -100이 됨을 알 수 있습니다.
여기서 sin값은 각도 표시를 일반각도가 아닌 호도법으로 했기 때문에
Radian으로 계산해야 합니다.
이와 같이 교류전원을 표현하려면 어떤 특정한 시간에
따라 값이 달라지기 때문에 그 크기를 표현하기 위해 어떠한 약속을 따로
정할 필요가 있게 됩니다.
그래서 나온 개념이 실효치인데요,
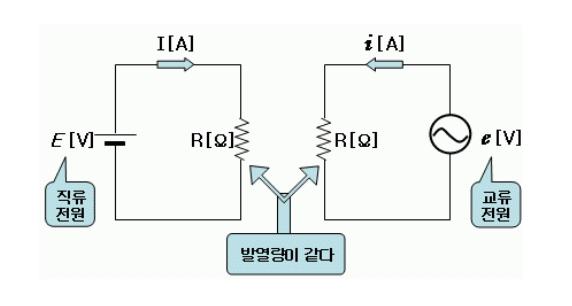
위 그림과 같이 동일 저항 R[Ω]에 직류 기전력과 교류 기전력을 가하면 저항체는 발열을 하게 됩니다. 이 때 발생된 열량이 서로 똑같다면 직류 기전력 E[V]와 교류 기전력 e[V]는 동일한 효과가 있는 것으로 보며, 실제(實際)로 효과(效果)가 있는 값이라는 점에서 이 때의 교류 기전력 e[V]를 실효치(實效値)라 합니다.
우리가 통상적으로 말하는 가정용 220V라든가 삼상 380V같은 교류 전원은 모두 실효치로 표기하기로 약속한 것이며 그 관계는 다음과 같습니다.
실효치 E = Em/√2 = 약 0.707Em[V] 여기서 Em은 순시치에서 거론했던 교류전압의 최대치를 의미합니다.
따라서 일반 가정용 220V라면 실제로 흐르는 순간 최대전압은
220 = Em / √2 ,
Em = 220 x √2 = 311.08[V] 가 됨을 알 수 있습니다.
각종 멀티테스터 같은 측정계기들 역시 교류전압, 전류에 대해서는 실효치값으로 지시하도록 만들어져 있습니다. 다만, 오실로스코프같은 파형을 직접 측정하는 계기는
순시치와 최대치를 측정할 수 있습니다.
평균치는
보시는 바와 같이 사인파 교류의 파형은 양과 음이 대칭되어 번갈아 변하기 때문에 이것을 계속 평균하면 0값이 됩니다.
그래서 아래의 그림처럼 양의 반주기 동안에 대해서만 평균을 취한 것이 평균치이며
최대치와의 관계는 다음과 같습니다.
Eav = 2/π Em = 약 0.637 Em 여기서 Em은 교류파형의 최대치입니다.

'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 교류회로 (Alternating Current Circuit)의 해석 (0) | 2020.11.09 |
|---|---|
| 직류회로(Direct Current)의 해석 (0) | 2020.11.06 |
| 전기전자 공학단위 정리 (0) | 2020.11.04 |
| 검출스위치 및 수동스위치의 종류 (0) | 2020.10.28 |
| 진상콘덴서의 용도 및 역할 (0) | 2020.10.26 |






