포톤 플럭스 (Photon Flux) / 분광 조사강도 (Spectral Irradiance)
포톤 플럭스 (Photon Flux) / 분광 조사강도 (Spectral Irradiance)

1. 포톤의 에너지 (Energy of Photon)
하나의 포톤은 λ로 표시하는 파장으로 그 성질을 나타내거나 아니면 E로 표시되는 등가의 에너지로 그 성질을 나타낸다. 포톤의 에너지 (E)와 빛의 파장(λ) 사이에는 다음의 반비례 관계식이 성립된다.
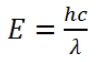
여기서 , h는 Planck 상수, c는 빛의 속도인데, 그 값은 아래와 같다.
· h = 6.626 × 10-34 joule·s
· c = 2.998 × 108 m/s
위 두 값을 곱하면, hc = 1.99 x 10-25 joules-m
위의 반비례 관계식은 에너지가 높은 포톤들(청색빛)로 구성된 빛의 파장이 짧다는 것을 의미한다. 낮은 에너지의 포톤들(적색 빛)로 구성된 빛은 파장이 길다. 포톤이나 전자와 같은 입자들을 다룰 때 보통 이용되는 에너지 단위는 Joule이 아닌 electron-volt(eV)이다. 1 eV는 하나의 전자를 1 V 올리는데 필요한 에너지인데 , 1 eV = 1.602 x 10-19 J 이다.
따라서 위 상수의 곱 hc를 eV의 항으로 표시하면, hc = (1.99 x 10-29 joules-m) x (1ev/1.602 x 10-19 joules) = 1.24 x 10-6 eV-m
위 값에서 파장 λ를 µm 단위로 하면 , hc = (1.24 x 10-6 eV-m) x(1.0 x 106 µm/m) = 1.24 eV-µm 포톤 에너지의 식을 eV와 µm로 표시하면 아래 식과 같이 흔히 사용되는 포톤의 에너지와 파장 사이의 관계를 얻게 된다.

1 × 106(hc/q)의 정확한 값은 1.2398 이나 대부분의 경우 반올림하여 1.24로 하여도 충분하다.
2. 포톤 플럭스 (Photon Flux)

< Fig01. 청색의 빛의 수는 적어도 에너지가 커서 동일한 빛의 세기가 가능 >
포톤 플럭스(photon flux)는 아래식과 같이 단위시간에 단위면적당의 포톤들의 수로 정의한다.

포톤 플럭스는 태양전지에서 생성되는 전자들의 수, 즉 전류를 결정하는데 중요하다. 포톤 플럭스가 포톤들의 에너지 (혹은 파장)에 대한 정보를 제공하지 않으므로 광원에서 포톤들의 에너지 혹은 파장에 대해 자세히 설명이 되어야 한다. 주어진 특정 파장에서 포톤의 에너지 (혹은 파장)와 포톤의 플럭스를 결합하면 특정 파장에서의 포톤들의 출력밀도를 계산할 수 있다.
출력밀도는 단일 포톤의 에너지에 포톤 플럭스를 곱하여 구한다. 포톤의 플럭스는 주어진 시간에 하나의 표면을 때리는 포톤들의 수를 나타내는 것이므로, 여기에 포톤 플럭스를 포함하는 포톤들의 에너지를 곱하면 단위 시간에 어떤 면을 때리는 에너지를 알 수 있는데, 이것이 출력밀도이다. W/m²의 단위로 출력밀도를 구하려면 포톤들의 에너지 단위가 Joules이어야 한다. 그 식은 아래와 같다.

여기서 , Φ는 포톤 플럭스, q는 전하(electronic charge)의 값으로 1.6 x 10-19 위 식이 내포하는 것은, 어떤 특정한 복사 출력밀도를 얻기 위해 필요한 높은 에너지 (짧은 파장)의 포톤들의 플럭스는 동일한 출력밀도를 얻기 위해 필요한 낮은 에너지 (긴 파장)의포톤 플럭스보다 더 작다는 의미이다. 애니메이션에서는 표면에 입사되는 복사 출력밀도가 청색 빛과 적색 빛 모두에서 같은데 , 청색 빛의 포톤들은 더 많은 에너지를 가지고 있으므로 소요되는 포톤들의 수가 더 적다는 것을 보여준다.
3. 분광 조사강도 (Spectral Irradiance)
F로 표기하는 포톤의 파장(혹은 에너지 )에 따른 분광 조사강도(spectral irradiance)는 광원의 특징을 설명하는데 가장 널리 사용되는 방법이다. 이는 특정 파장에서의 출력밀도를 나타낸다. 그 단위는 Wm-2µm-1이다. Wm-2는 파장 λ(µm)에서의 출력밀도이다. 그러므로 m-2는 발광체의 표면적을 나타내고, µm-1은 해당 파장이다.
태양전지를 분석하는 데는 분광 조사강도와 함께 포톤의 플럭스가 필요하다. 앞의 포톤의 플럭스에서 설명한 바와 같이 , 분광 조사강도는 주어진 파장에서 포톤의 플럭스를 W/m2로 변환하여 구할 수 있다. 그 결과는 아래 식과 같이 주어진 파장으로 나누어진 형태이다.

여기서 ,
· F : 분광 조사강도 (Wm-2µm-1)
· Φ : 포톤의 플럭스 (# photons m-2sec-1)
· E, λ 는 포톤의 에너지 (joule)와 파장(µm)
· q, h, c : 상수
분광조사강도는 보통 아래와 같이 파장의 함수로 나타낸다.
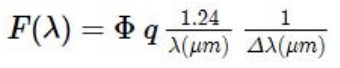
· F(λ) : 분광 조사강도 (Wm-2µm-1)
· Φ : 포톤의 플럭스 (# photons m-2sec-1)
· E, λ는 포톤의 에너지 (eV)와 파장(µm)
· q : 상수 (1.6 x 10-19)

< Fig02. 인공 광원의 분광 조사강도(왼쪽 축) / 자연 태양광의 분광 조사강도(오른쪽 축) 비교표 >
4. 복사에너지 출력밀도 (Radiant Power Density)
광원으로부터 방사된 전체 출력밀도는 분광 조사강도를 전 파장 영역 , 또는 전 에너지 영역에 걸쳐 적분하여 계산할 수 있다. 그러나 어떤 광원의 분광 조사강도에 대해 닫혀 있는 형식의 방정식은 존재하지 않는다. 대신에, 측정된 분광 조사강도를 측정한 파장 영역에 해당하는 파장을 곱하고, 이를 전 파장영역에 걸쳐 계산하는 방식이다. 다음 식은 어떤 광원으로부터 방사된 전체 출력밀도를 계산하는데 사용된다.
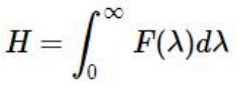
여기서 ,
· H : 광원으로부터 방사된 전체 출력밀도 (Wm-2)
· F(λ) : 분광 조사강도 (Wm-2μm-1)
· dλ : 파장
그러나 광원의 분광 조사강도를 표현하는 폐쇄 형태(closed form)의 방정식은 존재하지 않는다. 대신에 , 측정한 분광 조사강도에 측정 파장을 곱하는데, 이를 전 파장에 걸쳐 계산한다. 아래 방정식은 하나의 광원으로부터 방사되는 전체 출력밀도를 계산하는데 시용된다.

여기서 ,
· H : 광원으로부터 방사된 전체 출력밀도 (Wm-2)
· F(λ) : 분광 조사강도 (Wm-2μm-1)
· Δλ : 파장
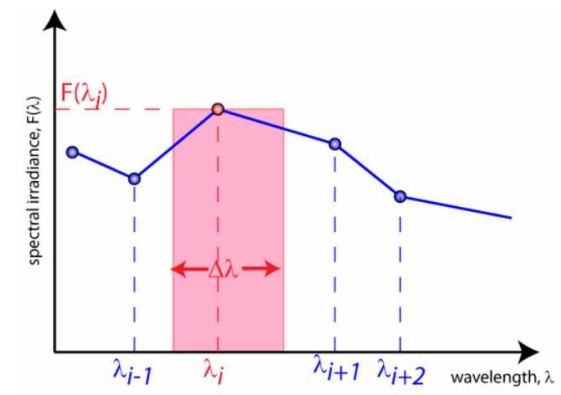
< Fig03. 광원의 전체 출력밀도 적분계산 >
보통, 측정된 스펙트럼은 방사(emission)와 흡수 라인들을 포함하기 때문에 매끄러운 모양이 아니다. 일반적으로, 파장구간은 균일하지 않은데 , 스펙트럼의 변화가 급격한 영역에서는 더 많은 데이터를 얻을 수 있도록 한다. 스펙트럼 폭(width)은 2개의 이웃하는 파장 사이의 중간점으로부터 계산한다.
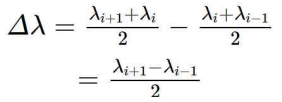
각 구간별 출력은 아래와 같다.

모든 구간의 값을 합하면 위 방정식에서의 출력밀도 H를 얻을 수 있다.
'공사교육자료 > 전기 - 공사교육' 카테고리의 다른 글
| 대기권 밖에서의 태양 복사 (Solar Radiation outside the Earth's Atmosphere) (0) | 2025.06.24 |
|---|---|
| 태양복사 및 흑체복사의 설명 (0) | 2025.06.23 |
| 태양빛의 기본원리 (0) | 2025.06.19 |
| 태양광발전(PV)의 개요 (0) | 2025.06.18 |
| 방송 조명기구의 종류 및 방송용 조명 기법 (0) | 2025.05.12 |






